Kouzla technické analýzy: Klouzavý průměr

Klouzavý průměr je nejstarším a stále základním indikátorem technické analýzy. Jak s ním nejlépe pracovat? Klouzavých průměrů je více a je třeba jeho výpočet správně nastavit. Jakým způsobem? Obchodovat jen na základě klouzavého průměru ale není dobré řešení.

V předchozím pilotním článku jsme vás krátce uvedli do problematiky indikátorů v technické analýze (TA). V následujícím seriálu vás budeme postupně seznamovat s nejdůležitějšími z nich.

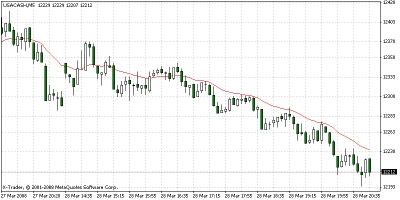
Pokud bychom měli určit, který z indikátorů je pro technickou analýzu  nejvýznamnější, pak určitě musíme mluvit o klouzavém průměru (anglicky: Moving Average, zkratka: MA). Tento indikátor patří  k nejstarším, ale zároveň k nejdůležitějším indikátorům technické analýzy, které byly kdy vytvořeny.

Význam klouzavého  průměru spočívá v jeho vyhodnocení býčí nebo medvědí nálady trhu. Ukazuje průměrnou cenu instrumentu za určité časové období. Jak se cena instrumentu v čase mění, klouzavý průměr se také mění, neboli roste či klesá.

Zjednodušeně řečeno klouzavý průměr vyhlazuje průběh ceny finančního instrumentu a díky tomu můžeme lépe pozorovat trend. Konstrukce tzv. jednoduchého MA je v zásadě primitivní a můžeme ji popsat matematickým vzorcem:

MA = (P1 + P2 + ……+ Pn)/n,

kde

P1 - n je cena, ze které počítáme průměr a
n je počet  časových úseků.

Časová řada cen  P1 - n je řada hodnot určité proměnné (ceny finančního instrumentu) uspořádaných v čase. Pro kurzy finančních instrumentů můžeme klouzavé průměry vypočítávat pro zavírací ceny, otevírací ceny, maxima, minima a jejich vzájemné kombinace. Obecně se doporučuje používat vždy zavírací ceny případně jejich kombinaci, protože zavírací ceny mají lepší vypovídací schopnost ohledně budoucí ceny instrumentu.

Existují čtyři základní druhy klouzavých průměrů: Jednoduchý, někdy také nazývaný Aritmetický (Simple, Arithmetic), Exponenciální (Exponential), Vyhlazený (Smoothed) a Lineárně vážený (Linear Weighted). Tyto jednotlivé druhy klouzavých průměrů se od sebe liší tím, že novějším pozorováním jsou  přiřazeny jiné váhové koeficienty.

Například u jednoduchého klouzavého průměru, jak vyplývá z výše uvedeného matematického vztahu, je všem hodnotám přiřazena stejná váha neboli důležitost. Z toho pak může vyplývat i určitý problém v interpretaci jednoduchého klouzavého průměru, pokud máme významné signály na počátku a na konci našeho časového úseku, který právě hodnotíme.

Exponenciální a lineárně vážené klouzavé průměry přiřazují naopak větší váhu novějším, tj. posledním hodnotám, takže tyto novější hodnoty více ovlivňují hodnotu klouzavého průměru za danou časovou periodu.

Poslední problém, který musíme vyřešit při použití klouzavého průměru, je jeho délka. Pokud zvolíme delší časový úsek, např. 365 na denním grafu, pak zjistíme, jaký byl převažující trend v uplynulých 365 dnech. Tento údaj je jistě zajímavý, ale málo použitelný pro samotné obchodování. Čím kratší naopak tento časový úsek volíme, tím nám křivka klouzavého průměru více vykresluje samotný instrument a přestává plnit svou hlavní funkci trendového indikátoru, tj. ukazovat směr trendu. Nedoporučuje se proto používat nižší hodnoty než 8.

Pro správnou volbu klouzavého průměru existují prakticky tři cesty. Všechny vycházejí zároveň z poznatku, že klouzavý průměr tvoří přirozenou hladinu supportu (podpory) v případě rostoucího trendu, respektive resistance v případě klesajícího trendu.

První z cest vychází z teorie a říká, že hodnota klouzavého průměru by se měla rovnat polovině dominantního tržního cyklu. Problém ovšem je, že dominantní tržní cyklus je velmi špatně identifikovatelný, navíc se trhy a tím i jejich dominantní cykly velmi často mění.

Druhá z cest je empirická – pokud uznáváme premisu, že klouzavý průměr tvoří přirozenou hladinu supportu, případně resistance pro daný instrument, pak tedy stačí nalézt takovou délku klouzavého průměru, která se vyznačuje nejvyšší četností kontaktu maxim, případně minim cenové svíčky s klouzavým průměrem.

Třetí z cest je spíše praktická. Pokud obecně finanční analytici hovoří o tom, že daný instrument se „blíží ke svému 20dennímu klouzavému průměru“, případně „instrument se odrazil od svého 20denního klouzavého průměru“, pak tato délka klouzavého průměru je přesně ta, kterou hledáme. Pokud totiž většina obchodníků předpokládá na určité cenové hladině problém pro postup svého instrumentu, pak se přirozeně v tomto místě a okolo něj hromadí nákupní a prodejní příkazy a je to tedy to správné místo, kudy by měl klouzavý průměr procházet.

Z výše uvedených poznatků pak můžeme odvodit i základní pravidla pro obchodování pomocí klouzavého průměru. Pokud exponenciální klouzavý průměr (EMA) roste, je to pro nás dobrý důvod ke vstupu do dlouhých pozic. Naše nákupní příkazy typu Buy Limit pak leží na klouzavém průměru a příslušný Stop Loss je pak lehce pod ním. Pokud EMA naopak klesá, je to dobrý důvod ke vstupu do krátkých pozic. Naše nákupní příkazy typu Sell Limit pak leží na klouzavém průměru a příslušny Stop Loss je pak lehce nad ním. 

Tento návod je samozřejmě silně orientační, dobrý obchodník potřebuje k tomu, aby vstoupil do pozice, více důvodů než jen fakt, že cenová svíčka dorazila ke klouzavému průměru.

Autor je analytikem společnosti X-Trade Brokers